Primzahlen in der asymmetrischen Kryptographie am Beispiel RSA Verfahren

Lesedauer: 9 Minuten

Immer wieder hört man von Erfolgen bei der Suche nach Primzahlen. Der bislang letzte bedeutende Meilenstein bei der Entdeckung großer Primzahlen wurde am 12. Oktober 2024 erreicht. An diesem Tag identifizierte der 36-jährige Hobbymathematiker Luke Durant aus San José, Kalifornien, die bisher größte bekannte Primzahl: 2136.279.841 - 1. Diese Zahl gehört zu den seltenen Mersenne-Primzahlen und hat 41.024.320 Dezimalstellen (bzw. Ziffern), was sie um rund 16 Millionen Stellen größer macht als der bisherige Rekordhalter aus dem Jahr 2018.

Der Aufwand und der Nutzen solcher Arbeiten und deren Erfolge erschließen sich nicht immer auf den ersten Blick, aber Primzahlen begegnen uns in unserem modernen Leben häufiger, als wir denken. So spielen Primzahlen beispielsweise in vielen kryptographischen Verfahren, insbesondere in der asymmetrischen Kryptographie, eine zentrale Rolle. Ihre Eindeutigkeit und ihre mathematischen Eigenschaften werden genutzt, um sichere Verschlüsselungen zu gewährleisten. Ein prominentes Beispiel ist das RSA-Verschlüsselungsverfahren, bei dem zwei große Primzahlen verwendet werden, um einen öffentlichen und einen privaten Schlüssel zu erzeugen. Die Übertragung dieser Website über das Internet ist beispielsweise mit dem RSA-Algorithmus verschlüsselt. Dasselbe gilt für das Online-Banking oder die Ende-zu-Ende-Verschlüsselung Ihres Messengers wie WhatsApp oder Signal.

Die Schwierigkeit, das Produkt großer Primzahlen in seine Faktoren zu zerlegen (Faktorisierungsproblem), macht die Entschlüsselung ohne den privaten Schlüssel extrem aufwändig und mit heutigen Mitteln praktisch unmöglich. Diese Probleme werden als Einwegfunktionen bezeichnet: Sie sind leicht in eine Richtung zu berechnen (z.B. Multiplikation von Primzahlen), aber extrem schwierig in die entgegengesetzte Richtung (z.B. Faktorisierung des Produkts in seine Primzahlen), was sie ideal für kryptographische Anwendungen macht.

Primzahlen im RSA-Verfahren

An einem Beispiel mit zwei kleinen Primzahlen soll dieses Verfahren noch einmal veranschaulicht werden:

• Primzahl: p = 53
• Primzahl: q = 61

Diese beiden Primzahlen multipliziert, ergeben das Produkt N:

N = p × q = 53 × 61 = 3233

Faktorisierung

N = 3233 wäre das öffentliche Produkt. Die Aufgabe des Angreifers besteht nun darin, das Produkt in seine Faktoren zu zerlegen (den beiden Primzahlen 53 und 61), um die Verschlüsselung zu knacken.

Eine Möglichkeit, das Produkt N zu faktorisieren, wäre, alle möglichen Primzahlen durch N zu teilen und zu prüfen, ob sie Rest 0 ergeben. Dazu müssten alle Primzahlen bis √3233 getestet. Warum √N​? Weil, wenn N ein Produkt zweier Zahlen ist, muss mindestens eine der beiden Zahlen kleiner oder gleich der Quadratwurzel von N sein. In unserem Fall ist √3233 ​≈ 56.85, also prüfen wir alle Primzahlen bis etwa 57. Die Primzahlen, die wir prüfen müssen, sind: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53.

3233 mod2 ≠ 0
3233 mod3 ≠ 0
3233 mod5 ≠ 0
3233 mod7 ≠ 0
...
3233 mod53 = 0

Teilt man nun 3233 durch 53 erhält man den zweiten Faktor 61.

In diesem Beispiel war es noch relativ einfach, das Produkt zu faktorisieren, da mit kleinen Zahlen gearbeitet wurde. In der realen Kryptographie wird die Faktorisierung durch die riesigen Primzahlen jedoch so aufwendig, dass man selbst durch Ausprobieren bekannter Primzahlen keine praktikable Lösung findet.

Primzahlsatz

Kryptographische Systeme wie RSA 2048 verwenden Primzahlen von etwa 1024 Bit. Für einen 2048-Bit-RSA-Schlüssel sind p und q typischerweise jeweils 1024 Bit lang. Eine Zahl von 1024 Bit hat 21024 verschiedene mögliche Werte, also eine Dezimalzahl etwa zwischen 10308 und 10309. Um die möglichen Primzahlen in dieser Menge zu berechnen, verwendet man den Primzahlsatz:

$$\pi(n) \sim \frac{n}{\ln n}$$

• Die Zahl ist etwa 10309 groß, da 21024 ungefähr diese Größenordnung hat:
  $$n = 1024 \times \log_{10}2 + 1 \approx \lfloor 309,25 \rfloor = 309$$
• Der Logarithmus von 10309 entspricht etwa 711:
  $$\ln(10^{309}) = 309 \ln⁡(10) ≈ 309 × 2,3 ≈ 711$$
• Das eingesetzt in den Primalzahlsatz ergibt:
  $$\pi(10^{309}) \sim \frac{10^{309}}{711} \sim 1,41 \times 10^{306}$$

Das bedeutet, dass es ungefähr 10306 Primzahlen im Bereich bis 10309 gibt. Das ist eine unvorstellbar große Zahl, bei der jeder Vergleich zum Scheitern verurteilt ist. Selbst wenn man jedes einzelne Atom des sichtbaren Universums als Speichereinheit verwenden würde, wäre dies um mehrere hundert Größenordnungen zu klein. Zum Vergleich: Das sichtbare Universum enthält etwa 1080 Teilchen.

Dies zeigt eindrucksvoll, wie aufwendig oder gar sinnlos es ist, alle möglichen Kombinationen auszuprobieren, um einen RSA-Schlüssel zu knacken. Selbst wenn intelligente Vorfilter eingesetzt werden, ist die Anzahl der möglichen Kombinationen immer noch exorbitant hoch. Selbst Supercomputer sind hier zum Scheitern verurteilt. Die Kompromittierung einer Verschlüsselung ist heute eigentlich nur noch durch Sicherheitslücken in der Implementierung oder durch den bewussten Einbau von Hintertüren möglich, die die Geheimnisse der Verschlüsselung preisgeben oder sogar ganz umgehen.

Erzeugen großer Primzahlen

Die Generierung großer, zufälliger Primzahlen für kryptografische Zwecke ist ein hochoptimierter Prozess, der auf effizienten Algorithmen und statistischen Methoden basiert. Während es tatsächlich extrem aufwändig wäre, alle möglichen großen Primzahlen zu finden, ist die gezielte Suche nach einer einzelnen großen Primzahl durch geschickte Techniken und Heuristiken gut machbar.

Zunächst wird eine große, zufällige Zahl generiert. Das geschieht in der Regel mit einem Zufallszahlengenerator, der kryptografisch sicher sein muss, um sicherzustellen, dass die Zahl tatsächlich zufällig und nicht vorhersagbar ist.

Die Erzeugung von Zufallszahlen ist ein potenzieller Schwachpunkt und spielt eine Schlüsselrolle in der Kryptographie. In klassischen Computern sind Zufallszahlen oft nur scheinbar zufällig, sie folgen grundsätzlich deterministischen Prozessen. Ihre Qualität hängt stark vom Algorithmus und der Entropiequelle (zufällige physikalische Ereignisse wie beispielsweise Mauszeigerkoordinaten oder Netzwerkrauschen) ab. Quantencomputer könnten einerseits echte Zufälligkeit liefern, da quantenmechanische Prozesse inhärent zufällig sind. Andererseits könnten sie Schwächen in klassischen Zufallszahlengeneratoren ausnutzen, was sie zu einer potenziellen Bedrohung für die klassische Kryptographie macht.

Die Länge der Zahl entspricht der gewünschten Bitgröße (z. B. 1024 Bit). Es kommen nur ungerade Zahlen in Betracht betrachtet, da gerade Zahlen (außer 2) keine Primzahlen sein können, was die Suche effizienter macht.

Die zufällig erzeugte Zahl wird dann auf ihre Primalität geprüft. Hier kommen spezielle Algorithmen zum Einsatz:

• Einfache Teilbarkeitstests: Zunächst wird geprüft, ob die Zahl durch kleine Primzahlen (z. B. die ersten 1000 Primzahlen) teilbar ist. Dies ist ein schneller Weg, um offensichtlich nicht-prime Zahlen auszuschließen.
• Wahrscheinlichkeitsbasierte Tests: Wenn die Zahl diese ersten Tests besteht, werden effizientere Algorithmen verwendet, die mit hoher Wahrscheinlichkeit feststellen können, ob eine Zahl prim ist. Die gebräuchlichsten Tests sind:
  • Miller-Rabin-Test: Ein probabilistischer Test, der feststellen kann, ob eine Zahl wahrscheinlich prim ist. Dieser Test wird mehrfach mit verschiedenen Parametern ausgeführt, um die Fehlerwahrscheinlichkeit extrem klein zu machen.
  • Fermatscher Primalitätstest: Ein schneller, aber weniger zuverlässiger Test, der oft als Vorfilter dient.
  • Baillie-PSW-Test: Eine Kombination aus verschiedenen Tests, die oft in praktischen Implementierungen verwendet wird.

Folgendes openssl-Kommando erzeugt z.B. in wenigen Sekunden eine Primzahl mit 1024 Bit Länge:

% openssl prime -generate -bits 1024
2757623931004800053211241421453390091725077232614149105276822132335258489063382140383785004403305794341340044911478
5011535071154571040577292775191592580213893096331518217510859072680080367635798840626302984026144193323450066781826
59109994766753537300107232446763023610228467674103237697315451893611477375017894487151

OpenSSL führt diesen Befehl bei der Erzeugung eines RSA-Schlüssels im Prinzip zweimal aus, um die beiden Primzahlen p und q für die Schlüsselerzeugung zu erhalten.

Erzeugung des RSA-Schlüssels

Nachdem die beiden Primzahlen p und q erzeugt wurden, können die nächsten Schritte zur Erzeugung eines RSA-Schlüssels durchgeführt werden. RSA besteht aus drei Hauptschritten: Berechnung des Modulus N, Auswahl des öffentlichen Exponenten
e und die Berechnung des privaten Exponenten d.

Modulus (N) berechnen

Modulus N ist das Produkt der beiden Primzahlen p und q:

$$N = p \times q$$

• N ist der Schlüsselparameter, der sowohl im öffentlichen als auch im privaten Schlüssel verwendet wird.
• Die Länge von N bestimmt die Bitlänge des RSA-Schlüssels. Für einen 2048-Bit-Schlüssel sollte N etwa 2048 Bit lang sein.

Eulersche ϕ-Funktion berechnen

Die Eulersche ϕ-Funktion (Totient) von N wird wie folgt berechnet:

$$\phi(N) = (p - 1) \times (q - 1)$$

Diese Funktion gibt die Anzahl der Zahlen kleiner als N an, die teilerfremd zu N sind, wobei N das Produkt der beiden Primzahlen p und q ist.

Zwei Zahlen sind teilerfremd, wenn nur die Zahl 1 beide teilt. Teilerfremde Zahlen haben keine gemeinsamen Primfaktoren.

Öffentlichen Exponenten (e) wählen

Der öffentliche Exponent e wird so gewählt, dass er:

Teilerfremd zu ϕ(N) ist, d. h. ggT(e,ϕ(N)) = 1

Ein kleiner Wert, der üblicherweise verwendet wird, ist e = 65537, weil er effizient zu berechnen ist und ausreichend Sicherheit bietet.

Privaten Exponenten (d) berechnen

Der private Exponent d ist der multiplikative Inverse von e modulo ϕ(N). Das bedeutet:

$$d \times e \equiv 1 (mod \phi(N))$$

Schlüsselpaare erstellen

• Der öffentliche Schlüssel besteht aus (N,e). Er wird veröffentlicht und kann von jedem genutzt werden, um Nachrichten zu verschlüsseln.
• Der private Schlüssel besteht aus (N,d). Er wird geheim gehalten und dient dazu, Nachrichten zu entschlüsseln.

Verschlüsselung und Entschlüsselung

Verschlüsselung:

Eine Nachricht M wird mit dem öffentlichen Schlüssel (N,e) verschlüsselt, wobei C die verschlüsselte Nachricht M ist:

$$C = M^e mod N$$

Entschlüsselung:

Die verschlüsselte Nachricht C wird mit dem privaten Schlüssel (N,d) entschlüsselt:

$$M = C^d mod N$$

Konkretes Beispiel

• Zu verschlüsselnde Nachricht M: 65
• Primzahl p = 61
• Primzahl q = 53
• N = p × q = 3233
• ϕ(N) = (p−1) × (q−1) = 60 × 52 = 3120
• Öffentlicher Exponent e: 65537 (oder ein kleinerer geeigneter Wert, z. B. e = 17)
• Privater Exponent d: d x e ≡ 1 (mod 3120)
  Mit e = 17, berechnet man d = 2753

Verschlüsselung:

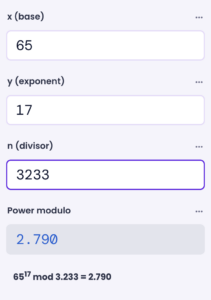
Für M = 65:

$$C = M^e mod N = 65^{17} mod 3233 = 2790$$

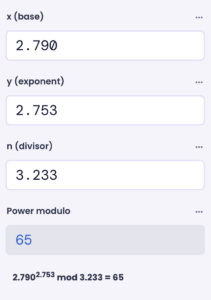
Entschlüsselung:

$$M = C^d mod N = 2790^{2753} mod 3233 = 65$$

Was es zu beweisen galt.